
Matteo Fadel, originario della provincia di Treviso, è oggi dottorando all’università di Basilea, in Svizzera, ed è il primo autore dello studio sul paradosso EPR pubblicato la settimana scorsa su Science. Fonte: www.unibas.ch
«Ho iniziato ad appassionarmi alla meccanica quantistica già dalle superiori», ricorda a Media Inaf Matteo Fadel, dottorando all’università di Basilea, in Svizzera, «quando mi sono reso conto dei suoi aspetti controintuitivi e delle sue implicazioni sul piano filosofico». Ebbene, ora che ha 28 anni, in tasca una laurea triennale in fisica presa a Padova e un master, sempre in fisica, al politecnico di Zurigo, quella passione è diventata un lavoro. E quegli aspetti controintuitivi – comprese le loro implicazioni filosofiche – sono diventati una sfida: il punto di partenza per approntare esperimenti di laboratorio. Esperimenti come quello che ha appena portato Fadel a firmare come primo autore un articolo pubblicato la settimana scorsa nientemeno che su Science. E che ha permesso, per la prima volta, di osservare uno fra i paradossi più noti della meccanica quantistica – il celebre paradosso Epr, dalle iniziali dei tre scienziati che nel 1935 per primi lo proposero: Albert Einstein, Boris Podolsky e Nathan Rosen – in un sistema formato da molte particelle. Quante? 590.
Cinquecentonovanta atomi di rubidio – più o meno 30, specificano gli autori del paper – raffreddati tramite un laser ad appena qualche miliardesimo di grado sopra lo zero assoluto a formare condensati di Bose-Einstein: “nuvole di atomi” in cui lo stato della materia è così particolare da far emergere proprietà quantistiche fra le più bizzarre. Prima fra tutte, quelle dell’entanglement, che fanno sì che due entità separate – fotoni, elettroni o altre coppie di particelle – si comportino, allorché sottoposte a una misura, come se fossero inscindibilmente connesse. Ebbene, nei condensati messi a punto da Fadel e colleghi le entità in stato di entanglement sono interi gruppi di atomi: è quello che si chiama entanglement distribuito. Ciò ha permesso ai ricercatori di misurare direttamente, tramite tecniche di imaging ad alta risoluzione, le correlazioni di spin tra parti separate spazialmente di un condensato di Bose-Einstein. E di osservare, per la prima volta fra più di due atomi, il cosiddetto steering: una proprietà dell’entanglement che consente di conoscere gli stati possibili di un sistema in una certa posizione compiendo una misura in un’altra posizione.
Il tutto – qui sta il bello – con un livello d’incertezza inferiore a quello previsto dal principio d’indeterminazione di Heisenberg, dimostrando così il paradosso Epr. Ed è proprio questo aspetto che abbiamo voluto approfondire con Matteo Fadel.
Fadel, com’è possibile “aggirare”, grazie all’entanglement, il principio di indeterminazione di Heisenberg? Che collegamento c’è fra questi due pilastri della meccanica quantistica?
«Il legame tra entanglement e indeterminazione è delicato, provo a spiegare le cose dal principio. Lo scopo di una teoria fisica è di descrivere un sistema al punto da riuscire a predire il risultato delle misure compiute su di esso. Una delle caratteristiche principali della meccanica quantistica è che essa fornisce solo predizioni probabilistiche per i risultati delle misure. Inoltre, il principio di indeterminazione di Heisenberg mostra che alcune coppie di proprietà non possono essere predette con precisione arbitraria, ma esiste bensì un limite ultimo alla loro conoscenza simultanea. Per fare un esempio, se fossimo in grado di prevedere accuratamente la posizione di una particella allora saremo incerti sulla sua velocità, e viceversa.
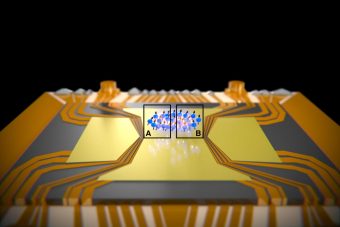
Una nuvola di atomi intrappolata su un chip da campi elettromagnetici. Il paradosso Epr è stato osservato tra le regioni spazialmente separate A e B. Crediti: University of Basel, Department of Physics
Agli albori della meccanica quantistica una domanda cruciale consisteva nel capire se questa “indeterminazione” fosse solamente imposta dalla teoria (perché incompleta o solo parzialmente esatta) o un vero limite imposto dalla Natura (come adesso si sa). Einstein, Podolski e Rosen idearono un esperimento mentale per cercare di trovare risposta a questo dilemma. Considerarono due particelle, A e B, in uno stato particolare permesso dalla meccanica quantistica, e mostrarono che il principio di indeterminazione applicato al sistema B poteva essere violato! L’idea consiste nel fatto che misurando posizione o velocità della particella A si è in grado di sapere il risultato di una misura della stessa grandezza su B, apparentemente violando il principio di indeterminazione. Basandosi su questa osservazione, Einstein, Podolski e Rosen conclusero (erroneamente) che la meccanica quantistica era una teoria incompleta, e (sempre erroneamente) che il principio di indeterminazione imponeva un limite solo apparente».
Perché erroneamente? Quale sarebbe la conclusione corretta?
«La conclusione corretta consiste nel fatto che le due particelle considerate, A e B, sono in uno stato tale per cui non possono essere considerate sistemi fisici distinti, ma costituiscono un unico sistema. Stati di questo tipo sono stati nominati da Schrödinger “entangled”. Il principio di indeterminazione applicato localmente ad una particella può essere violato grazie alla presenza di correlazioni con altre particelle del sistema stesso, nonostante il principio di indeterminazione applicato al sistema intero resti comunque valido».
E questa violazione fino a che punto si può spingere?
«Idealmente, il principio di indeterminazione applicato a un sistema può essere aggirato completamente se questo è in uno stato entangled con un altro sistema. Con questo intendo che risultati di misure diverse possono essere predette con esattezza, apparentemente violando il principio di indeterminazione».
Ci può fare un esempio, magari riferendosi proprio al vostro esperimento?
«Il fatto che A e B siano due sistemi entangled permette di prevedere il risultato di una misura su B basandosi sul risultato di una misura compiuta su A. Se il sistema A non fosse accessibile, i risultati delle misure su B apparirebbero casuali, e non sarebbero prevedibili. Nel caso del nostro esperimento abbiamo riprodotto l’esperimento mentale proposto da Einstein, Podolski e Rosen con centinaia di particelle. Nel nostro caso, A e B sono due insiemi di atomi in uno stato entangled. Misurando lo spin degli atomi del gruppo A possiamo prevedere quale sarà lo spin degli atomi nel gruppo B, dimostrando che il principio di indeterminazione per B può essere violato grazie all’informazione ottenuta da una misura su A».
Per saperne di più:
- Leggi su Science l’articolo “Spatial entanglement patterns and Einstein-Podolsky-Rosen steering in Bose-Einstein condensates“, di Matteo Fadel, Tilman Zibold, Boris Décamps e Philipp Treutlein






