Se cerchiamo il termine “crisi” nel dizionario, troviamo che – in un contesto economico, politico o sociale – essa denota un’uscita improvvisa e traumatica da uno stato di equilibrio seguita da uno stato più o meno permanente di disorganicità, mancanza di uniformità e coerenza. Anche nel mondo scientifico si può entrare in crisi: succede quando viene messa in discussione una teoria, una credenza, un modello invalso. È quanto successo, ad esempio, nel 2019, dopo che alcuni cosmologi, analizzando nelle mappe Planck – il satellite incaricato di misurare le fluttuazioni della radiazione cosmica di fondo con una precisione senza precedenti – il lensing gravitazionale e altri parametri, erano giunti a proporre l’ipotesi che l’universo avesse curvatura positiva. O meglio: che non fosse possibile considerarlo piatto senza introdurre una “tensione” – una crisi, appunto – nella cosmologia. Fra chi ha deciso di affrontare il problema e cercare una soluzione c’è Sunny Vagnozzi, un giovane ricercatore italiano originario di Terracina, in provincia di Latina, che deve il proprio nome al sole che splendeva il giorno della sua nascita, dopo settimane di incessante pioggia. Amante delle stelle sin da piccolo grazie alla madre (di origine taiwanese) e al padre, a 17 anni si è trasferito a Trento per studiare fisica, per poi trascorrere un periodo a Londra, e ancora in Australia, Danimarca, Svezia, e infine a Cambridge. Viaggiatore nel mondo così come nella fisica, ha cominciato la sua carriera studiando le particelle elementari e si trova ora a voler capire che forma ha l’universo nel suo insieme, che cosa contiene e come è evoluto nel passato, nel presente e nel futuro. Media Inaf l’ha intervistato per farsi raccontare la storia di questa crisi cosmologica e di come sia stata risolta.
Come è nata l’idea di questo studio?
«Dopo il paper di Di Valentino, Melchiorri e Silk pubblicato su Nature Astronomy nel 2019 – che portava alla luce i risultati e i problemi sollevati da Planck – c’è stata molta discussione nel campo su quali fossero le implicazioni dei loro risultati, e il mondo della cosmologia, semplificando un po’, è come se si fosse spaccato in due: da un lato, chi diceva che i risultati non potevano essere corretti e l’universo non poteva essere sferico – certamente non così tanto sferico come suggerivano i dati; altri che dicevano che bisognava dar loro più credito, che non fosse il caso di nascondere queste anomalie sotto al tappeto. Io, anche per motivi personali, mi trovo un po’ a metà strada».
In che senso?
«Da un lato collaboro con gli altri autori di quell’articolo di Nature Astronomy – e ho ascoltato e studiato attentamente il loro lavoro – dall’altro lato lavoro qui a Cambridge, circondato da persone che lavorano su Planck e che dicono che non vi sono dubbi, che l’universo è piatto e Planck non riporta anomalie. Entrando nel dettaglio, il problema è il seguente: se prendiamo i dati di Planck da soli, questi direbbero effettivamente che l’universo è chiuso (o sferico) – e tra l’altro direbbero che è molto sferico, perché la curvatura viene rivelata con un livello di confidenza superiore al 99 per cento. Un risultato, per certi versi, davvero sorprendente».
Quindi, l’universo può essere più o meno sferico? Che significa?
«Sì, c’è un parametro – il parametro di curvatura Omega-k – che quantifica quanto l’universo si discosta dall’essere piatto. Omega-k uguale a zero significa universo perfettamente piatto, valori negativi significano universo curvo, sempre più curvo quanto più negativo il valore del parametro. Possiamo pensare che l’inverso di Omega-k sia il raggio di curvatura e, quindi, più Omega-k cresce verso valori negativi più l’universo è curvo su una scala piccola. Funziona bene se lo paragoniamo alla Terra: noi non percepiamo la curvatura terrestre perché la scala su cui essa si piega è troppo grande per i nostri occhi. La scala che suggerisce Planck è invece molto piccola in senso relativo – parliamo pur sempre dell’intero universo».
Piccola tanto da potersene accorgere direttamente?
«Sì, così piccola che Planck lo ha visto. O almeno questo secondo alcuni».
Dove sta il problema, dunque?
«Il problema è che, se prendi le misure effettuate da Planck sulla radiazione cosmica di fondo, è difficile riuscire a credere al valore di curvatura che si estrae. C’è un motivo subdolo che si chiama “degenerazione geometrica”, e provo a spiegartelo con un esempio che uso spesso ed è molto attinente all’esperienza quotidiana. Immagina di vedere l’immagine di una persona su uno sfondo completamente bianco, ecco lei è la nostra radiazione cosmica di fondo: in particolare, la sua distanza da noi rappresenta la distanza fra noi e il fondo cosmico, mentre la sua altezza è il cosiddetto orizzonte sonoro – cioè la massima lunghezza percorribile dalle onde sonore nell’universo primordiale. Le onde sonore, infatti, iniziano a propagarsi pochi istanti dopo la nascita dell’universo e si interrompono quando si forma il fondo cosmico a microonde. Tornando alla nostra persona decontestualizzata, se la guardiamo così com’è non riusciamo a dire contemporaneamente quanto è alta e quanto è lontana: ci sono infinite combinazioni di distanza e altezza che sottendono, ai nostri occhi, lo stesso angolo. Abbiamo, per dirla in matematichese, una sola equazione con due variabili».
Non si può risolvere.
«Esatto. Se vogliamo capire, poi, quanto è curva la Terra fra noi e questa persona dobbiamo riuscire a distinguere e misurare queste due variabili – altezza e distanza – separatamente. L’angolo da solo non basta, bisogna aggiungere dei riferimenti fra noi e la persona. Potremmo posizionare questa persona nel contesto di un viale alberato, ad esempio, e sfruttare i riferimenti forniti dagli alberi».
Come si collega questo alla radiazione cosmica di fondo misurata da Planck?
«Nel caso della radiazione cosmica di fondo – chiamiamola Cmb – gran parte dell’informazione che abbiamo viene dallo spettro di potenza. È questo l’osservabile che misura Planck, e ci dice quanto le fluttazioni della Cmb sono correlate guardando due punti separati da scale angolari più o meno grandi (più vado verso destra, nel grafico qui sotto, più l’angolo sotteso è piccolo). L’elemento più importante di questo spettro è il primo picco, quello più alto, perché è una delle impronte lasciate dalle onde sonore nell’universo primordiale: trattandosi di oscillazioni armoniche, corrisponde all’armonica fondamentale. Ci sta dicendo, per tornare all’esempio di prima, che i nostri occhi vedono la persona sotto un angolo di un grado. Quindi, per capire quanto è curvo l’universo – a questo punto – ci servono degli alberi fra noi e la persona.
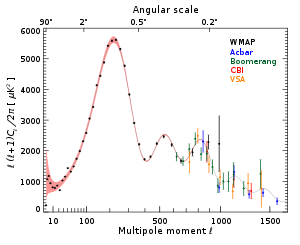
Spettro di potenza della radiazione cosmica di fondo a microonde in termini di scala angolare (sull’asse delle x). I dati mostrati provengono dagli strumenti Wmap (2006), Acbar (2004) Boomerang (2005), CBI (2004), e Vsa (2004). La linea continua mostra un modello teorico.
E cosa sono gli “alberi”, nell’universo?
«Gli alberi sono degli osservabili, nell’universo, che fungono da righelli cosmici. Tradizionalmente, le oscillazioni barioniche acustiche – Bao. Si confronta la lunghezza nota di questi righelli con quella apparente in cielo, e dal confronto si calcola la distanza dei righelli. Se ne misuro un numero sufficiente, riesco a definire quanto lontana è la Cmb».
Quindi ci sta dicendo che la distanza fra noi e la radiazione cosmica di fondo non è conosciuta, se capisco bene. Credevo che il suo redshift fosse ben noto…
«Esatto, occorre conoscere la sua distanza – comunque quantità direttamente collegate alla distanza, come il tasso di espansione dell’universo nelle varie epoche cosmiche. Quello che conosciamo precisamente è, appunto, il redshift della Cmb. Se prendiamo l’informazione che proviene dalla Cmb, la luce, questa parte con una certa energia – o lunghezza d’onda – e per effetto dell’espansione dell’universo, durante il suo viaggio nelle epoche cosmiche perde energia – o viene stiracchiata, se pensiamo alla forma di un’onda. Quanta energia perde – o di quanto si dilata la sua lunghezza d’onda – dipende, appunto, dal redshift. La distanza, invece, non è necessariamente una quantità nota: per conoscerla, dovremmo sapere quanta materia c’è fra noi e la Cmb, quanta energia oscura, quanta curvatura e qual è il tasso di espansione attuale (H0, la costante di Hubble). Diventa un problema un po’ circolare: se vogliamo dire quanto lontana è, dobbiamo assumere un certo modello cosmologico e determinati valori per i parametri detti sopra. Quel che noi vogliamo fare, invece, è l’opposto: usare la Cmb per definire come è fatto l’universo».
Torniamo alla curvatura, allora.
«Certo. Dicevamo che sì, è possibile ottenere una misura di curvatura usando solamente la Cmb, ma – primo problema – questa misura non sarà precisa per via della degenerazione geometrica e – secondo problema – probabilmente non sarà nemmeno affidabile, cioè accurata. Bisogna rompere la degenerazione geometrica: questo ci porta al problema sollevato dal paper di Di Valentino et al.».
Quale?
«Si può provare a rompere questa degenerazione usando le Bao, ad esempio, e facendolo si ottiene come risultato che l’universo è piatto. Il problema è che, nel contesto di un universo non piatto, i risultati provenienti dalle Bao e da Planck – dalla Cmb, quindi – sono molto in tensione, e diventano non confrontabili. E se due dati vogliono due cose molto diverse, la verità – in cosmologia – non sta nel mezzo. In parole semplici, Cmb e Bao non possono essere combinati».
Facciamo un passo indietro. Nel paper di Di Valentino e colleghi, però, vengono usate proprio le Bao. Non è corretto il loro procedimento, dunque?
«Loro hanno usato le Bao, esattamente, ma proprio per portare alla luce questa tensione. Il ragionamento seguito nel loro lavoro è il seguente: i risultati di Planck vorrebbero un universo molto sferico, le Bao insieme a Planck vogliono un universo piatto. Problema risolto? No, perché in realtà non possiamo metterle insieme».
È per questo che loro asseriscono che l’universo sia sferico?
«Non proprio: loro non dicono che l’universo è sferico. Dicono piuttosto che questi risultati di Planck portano alla luce delle tensioni e aprono una crisi nella cosmologia. Questo è il messaggio che ha generato disaccordo e discussioni nella comunità».
Planck, comunque, è il satellite che finora ha misurato la Cmb nel modo più preciso finora…
«Se intendiamo “preciso” nel senso che ha riportato barre d’errore sulle misure molto piccole, allora sì, sono d’accordo. Se invece vogliamo dire accurato, cioè centrato sul valore giusto, allora molti sono d’accordo sul fatto che, per quanto riguarda la curvatura, Planck non sia stato accurato».
Spieghiamo meglio questa incompatibilità, però. Se prima dicevamo che Planck da solo non può misurare la distanza della Cmb, e che occorrono dei righelli – come le Bao – che aggiungano dei riferimenti adeguati, com’è che ora le Bao non vanno più bene?
«Perché bisogna trovare dei righelli adeguati. Le Bao sono un esempio, ma in questo caso non sono il righello giusto. Si possono combinare due metodi solo se le informazioni che danno da principio non sono troppo discordanti».
Cosa manca alle Bao per essere il righello giusto?
«Non direi che manca loro qualcosa. Direi piuttosto che, nel caso di Planck, e soprattutto nel contesto di un universo non piatto, non vanno bene. Quando noi facciamo cosmologia, dobbiamo sempre e comunque assumere un certo modello di universo a priori. Quindi, quando parlo di accordo fra due misure, ne parlo in relazione al modello adottato. In questo caso, se consideriamo un modello di universo piatto, allora le Bao sono il righello giusto e posso combinarle con la Cmb. Questo è quello che hanno fatto alcuni satelliti prima di Planck (come Wmap, ad esempio). Se invece cambio contesto, e non mi fisso su una curvatura piatta ma le consento di variare, allora non possiamo più confrontare questi due metodi. Ecco il messaggio del paper di Di Valentino et al.: quando voglio combinare due misure, devo essere sicuro che abbia senso farlo nel contesto in cui mi trovo».
Veniamo al vostro lavoro. Se ho capito bene, voi avete usato un altro metodo per stimare la curvatura, e questo metodo vi porta al risultato di un universo piatto, senza scontrarsi con nessuna delle due fazioni di cui parlavamo prima. Avete dunque risolto questa crisi cosmologica?
«Noi siamo riusciti a trovare quello che in inglese chiameremmo golden dataset, che ci ha permesso di mettere dei righelli fra noi e la Cmb senza entrare in forte tensione con Planck, nel contesto di un universo non piatto. L’obiettivo era quindi vedere se i nostri “cronometri cosmici” – così abbiamo chiamato i nostri righelli – ci potevano aiutare a stimare la curvatura e risolvere le tensioni».
Cosa sono questi cronometri cosmici?
«Possiamo pensarli come il ticchettio dell’universo: sono degli oggetti che ci sanno dire quanto invecchia l’universo al variare del redshift. Sappiamo che più il redshift è alto, più guardiamo indietro nel tempo: ma quanto lontano? Lo scopo dei cronometri cosmici è, in seconda istanza, misurare il tasso di espansione dell’universo nel presente e nel passato – fino a un redshift circa pari a due, direi un terzo della distanza fra noi e la Cmb, la stessa distanza che si raggiunge anche con le Bao. È molto difficile, però, trovare dei cronometri cosmici adeguati».
E, precisamente, di che oggetti parliamo?
«Si tratta di galassie passive e molto massicce, che si sono formate molto anticamente e hanno avuto una storia di formazione stellare molto breve. Da allora, hanno continuato a evolvere passivamente. Quel che facciamo noi è misurarne l’età in funzione del redshift – osservando molte di queste galassie in diverse epoche cosmiche – e dalla loro differenza di età risaliamo al tempo intercorso e al tasso di invecchiamento dell’universo».
State quindi assumendo che queste galassie, osservate a diverse distanze da noi, siano tutte parte della stessa primordiale famiglia?
«Sì, esattamente, anche se in realtà imparentiamo galassie fra loro molto vicine in redshift. Esiste una relazione che lega età dell’universo, redshift e tasso di espansione, e il nostro scopo è quello di invertirla per ricavare il tasso di espansione dell’universo nel tempo. Per fare questo, però, siccome la relazione si può invertire solo considerando piccole differenze in età e redshift (è una relazione differenziale), ci occorrono galassie molto vicine le une alle altre. Questo lavoro di collezione del campione, selezione delle galassie giuste e analisi delle loro proprietà per calcolare l’età è stato fatto da un nostro coautore esperto, Michele Moresco. Lui ha passato gran parte della sua carriera cercare questi cronometri cosmici, e a dimostrare che possiamo usarli in maniera robusta».
Quando è nato questo concetto di cronometro cosmico?
«È un’idea nata alcuni anni fa – la prima pubblicazione risale al 2002, sono passati ormai vent’anni – ed è stata proposta da due scienziati fra cui proprio il secondo autore del nostro studio, Avi Loeb. Lui è davvero un genio, un pozzo di idee. Ha proposto moltissimi studi e fatto predizioni cosmologiche che poi si sono rivelate corrette, oltre agli altri studi meno tradizionali per i quali è noto – come ad esempio quello sui dinosauri o sui possibili segni di vita aliena».
Come avete capito che queste galassie sono il righello giusto?
«Semplicemente, abbiamo provato. Abbiamo provato a confrontare le due misure e abbiamo visto che non erano in disaccordo nel contesto di un universo non piatto – o meglio, non fissando a priori alcun parametro di curvatura. Nonostante ciò, quando poi siamo andati a misurare il parametro di curvatura risultante dalla combinazione delle due misure, abbiamo trovato che è consistente con un universo piatto entro le barre d’errore. Questo ci porta finalmente alla nostra conclusione: è vero che Planck vuole un universo sferico, ma è anche importante aiutare la misura proveniente dal solo Planck in un modo adeguato e che non entri in tensione con esso: i nostri cronometri cosmici. Facendolo, troviamo un universo piatto».
Si tratta di un risultato definitivo o va perfezionato?
«Noi speriamo che già da ora questo risultato ponga fine alla diatriba cosmologica generata dai dati di Planck. C’è comunque margine di miglioramento nelle misure e nei risultati, questo è innegabile. Ci saranno altri esperimenti di Cmb dopo Planck – parliamo dell’Atacama cosmology telescope ad esempio, del Simons observatory e di Cmb-S4 – e poi esiste un altro metodo, completamente indipendente da qualunque modello cosmologico, che consente di ricavare la curvatura. Ci stiamo lavorando e i risultati sono buoni, magari ve li racconto appena pubblichiamo l’articolo».
Per saperne di più:
- Leggi su The Astrophysical Journal l’articolo “Eppur è piatto? The cosmic chronometer take on spatial curvature and cosmic concordance”, di Sunny Vagnozzi, Abraham Loeb e Michele Moresco







