
Interferometro di Sagnac costruito con 2 chilometri di fibre ottiche avvolte intorno a un telaio quadrato di alluminio di 1,4 metri di lato. Crediti: R. Silvestri
Un gruppo di ricercatori della Università di Vienna ha condotto un esperimento pionieristico in cui ha misurato l’effetto della rotazione della Terra su fotoni entangled. Il lavoro, appena pubblicato su Science Advances, rappresenta un risultato significativo che spinge i confini della sensibilità alla rotazione nei sensori basati sull’entanglement quantistico, ponendo potenzialmente le basi per ulteriori esplorazioni al confine tra meccanica quantistica e relatività generale.
L’esperimento ha impiegato un interferometro ottico di Sagnac, tra i dispositivi più sensibili alle rotazioni. Tali interferometri sono stati cruciali per la comprensione della fisica fondamentale fin dai primi anni del secolo scorso, contribuendo ad affermare la teoria della relatività speciale di Einstein. Oggi, la loro impareggiabile precisione li rende lo strumento definitivo per misurare le velocità di rotazione, limitato solo dai confini della fisica classica.
Per comprendere il funzionamento di questi dispositivi e la misura effettuata, abbiamo intervistato Raffaele Silvestri, primo autore dello studio, dottorando all’Università di Vienna nel gruppo di ottica quantistica sperimentale diretto da Philip Walther, gruppo che si occupa principalmente di scienza dell’informazione e computazione quantistica, fondamenti della teoria quantistica e investigazione dell’interfaccia fra la meccanica quantistica e la gravità generando e utilizzando stati quantistici della luce, come l’entanglement a più fotoni.
Gli interferometri che utilizzano l’entanglement quantistico hanno il potenziale per infrangere i limiti della fisica classica. In che modo?
«Gli interferometri “classici” (ovvero che non utilizzano stati quantistici della luce, come ad esempio la luce laser) sono limitati nella precisione di misura dello sfasamento indotto (da qualsivoglia effetto che si voglia misurare) sui fasci di luce che si propagano nei due percorsi (o bracci) dell’interferometro da un limite chiamato di shot-noise (shot-noise limit). Questo limite è proporzionale all’inverso della radice quadrata del numero di fotoni rilevati dal detector in un certo intervallo di tempo, un risultato che proviene banalmente dalla statistica dei conteggi di un processo random a variabili indipendenti, statistica che segue una distribuzione di Poisson (numero di conteggi/fotoni rilevati: N, incertezza o shot-noise: sqrt(N), incertezza relativa o shot-noise limit: 1/sqrt(N)). Ora, si possono sfruttare stati della luce in cui i fotoni invece che essere indipendenti condividono delle correlazioni quantistiche, andando quindi a modificare la statistica dello stato della luce. L’esempio più celebre è quello dello squeezing quantistico (statistica sub-poissoniana), in cui le correlazioni dello stato di luce inviato nell’interferometro possono essere controllate in modo tale da ridurre l’incertezza sulla misura della fase (a discapito di un’incertezza maggiore sull’ampiezza del campo di luce, quindi dell’intensità o numero di fotoni per unità di tempo). Questa tecnica è stata utilizzata dagli interferometri rilevatori di onde gravitazionali delle collaborazioni Virgo e Ligo, riuscendo nella pratica a migliorare la precisione della misura della fase relativa indotta dalla fluttuazione spazio-temporale fra i due bracci di un interferometro di tipo Michelson. Come lo squeezing, anche l’entanglement fra le particelle (fotoni) che compongono uno stato quantistico può essere utilizzato per migliorare la precisione nella misura della fase interferometrica».
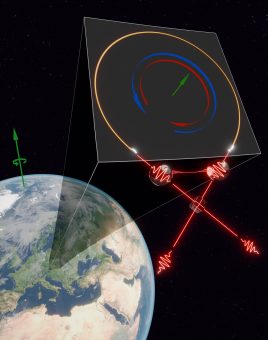
Illustrazione dell’esperimento: lo schema interferometrico di Sagnac a fibra (visualizzato all’interno di un inserto), è collocato a Vienna, in Austria, sulla Terra in rotazione. Due fotoni indistinguibili incidono su un cubo che divide il fascio, si crea un entanglement tra di essi e poi vengono accoppiati nell’interferometro a fibra. Crediti: M. Di Vita
In che modo?
«Per intuire la ragione fondamentale di tale fenomeno, consideriamo di avere uno stato di N particelle (fotoni) che sono entangled tramite il grado di libertà della loro posizione (path-entangled) all’interno dell’interferometro. Il caso fondamentale è rappresentato dallo stato NOON, ovvero una sovrapposizione quantistica in cui N fotoni si propagano in un braccio dell’interferometro (a) e 0 nell’altro (b) e viceversa (|N>a|0>b+|0>a|N>b). Lo stato quantistico con N fotoni in un modo spaziale (braccio) |N>a acquisterà al termine della propagazione N volte la fase rispetto a quella che avrebbe acquistato se solo 1 fotone si fosse propagato attraverso lo stesso percorso, (|N>a –> exp(i*N*phi)|N>a, mentre se N=0, |0>a –> exp(i*0*phi)|0>a = |0>a )). Lo stato entangled complessivo quindi acquisterà N volte la fase relativa rispetto al caso in cui solo un singolo fotone fosse stato inviato nell’interferometro (questo è dovuto all’evoluzione unitaria di uno stato di N bosoni in un singolo modo in questo caso spaziale). La precisione sulla misura di fase sarà invece un fattore sqrt(N) più precisa. Difatti, le frange d’interferenza incrementeranno la frequenza di N volte (il periodo della figura di interferenza è ridotto di N volte, 2Pi/N) e nel punto di massima sensibilità dell’interferometro (altrimenti detto punto di quadratura) la pendenza della funzione sarà N-volte maggiore, quindi aumentando considerevolmente la reazione dell’intensità o numero di fotoni rilevati rispetto a piccoli cambiamenti di fase. In linea di principio utilizzando stati NOON, che sono massimamente entangled, si può raggiungere il limite di precisione di Heisenberg, ovvero la soglia ultima di precisione raggiungibile in un interferometro dettata dalle leggi della meccanica quantistica (lo scaling è 1/N invece di 1/sqrt(N), un miglioramento di un fattore sqrt(N)). Questo effetto è anche chiamato super-risoluzione, ed è puramente dovuto alla presenza di questo particolare tipo di correlazione quantistica o entanglement fra N particelle (fotoni) e i due modi spaziali di propagazione. Purtroppo, nella realtà questo limite è molto difficile da raggiungere per via della decoerenza che questi stati quantistici subiscono nell’interazione con l’ambiente».
Come fate a dire che le particelle/fotoni sono entangled?
«La firma incontrovertibile della presenza dell’entanglement fra i due fotoni generati e i due modi spaziali all’interno dell’interferometro (senso di propagazione orario e antiorario in un interferometero Sagnac) è data dalla forma delle frange d’interferenza. In particolare dal raddoppiamento della frequenza o dimezzamento del periodo di oscillazione della curva d’interferenza rispetto al caso in cui singoli fotoni fra loro indipendenti e non correlati quantisticamente sono stati inviati nell’interferometro (effetto di super-risoluzione). Il fatto che la qualità dell’entanglement generato è invece quantificabile dalla visibilità o contrasto delle frange di interferenza, visibilità che è rimasta praticamente invariata prima e dopo la propagazione nell’interferometro ad un valore di circa 97 per cento. A essere precisi, si può ottenere l’effetto di super-risoluzione andando a utilizzare fotoni di lunghezza d’onda minore (metà di quella di riferimento in questo caso, ovvero 1550 nm / 2 = 775 nm ). Tuttavia, sono stati utilizzati fotoni generati dallo stesso processo (Spdc o spontaneous parametric down-conversion) sia per la misura a singolo fotone che per quella a due fotoni, ma solo dopo essere stati tutti filtrati alla lunghezza d’onda selezionata (1550 nm o lunghezza d’onda telecom), assicurando senza ombra di dubbio che la lunghezza d’onda dei fotoni fosse sempre la stessa in entrambe le misure. Non può esservi quindi altra spiegazione se non la presenza di entanglement nella misura a due fotoni».
Il salto di qualità nella sensibilità finora è sempre stato ostacolato dalla natura delicata dell’entanglement ma il vostro esperimento ha fatto la differenza. Ci può spiegare come?
«Uno stato NOON a due fotoni (N=2) è molto fragile e soggetto a decoerenza (e la sua fragilità aumenta esponenzialmente con il numero N di fotoni entangled) dove il contributo principale è dato dalla perdita di fotoni durante l’interazione con l’ambiente circostante, nel nostro caso la propagazione in una fibra ottica lunga 2 chilometri. Ad esempio, se l’interferometro trasmette il 10 per cento della potenza iniziale (o del numero totale di singoli fotoni indipendenti inviati), il numero di stati NOON a due fotoni che sopravvivrà alla propagazione sarà solo l’1 per cento ( (0,1)^N = (0,1)^2 = 0,01 ) degli stati generati. Tuttavia, la sensibilità di una misura di rotazione con un interferometro Sagnac è direttamente proporzionale al tempo di propagazione dei fotoni (lunghezza della fibra ottica) e all’area chiusa dell’interferometro (area circoscritta dal percorso chiuso). Più è grande e più sarà capace di risolvere una rotazione molto lenta, dove il fattore di proporzionalità fra la velocità di rotazione e la fase indotta (osservabile misurata) prende il nome di fattore di scala. È quindi estremamente impegnativo effettuare misure di precisione in interferometri di grandi dimensioni (grandi fattori di scala) utilizzando questi stati, poiché richiede la misurazione di una quantità significativa di questi (coppie di fotoni entangled che sopravvivono alla propagazione in una lunga fibra ottica) e della massima qualità possibile (la forza dell’entanglement è inizialmente elevata e si conserva dopo la propagazione)».
Come avete superato questi ostacoli?
«Abbiamo superato questi ostacoli aumentando, con una tecnica innovativa per questo scenario di applicazione, la stabilità nel tempo del nostro interferometro (area effettiva di oltre 700 metri quadrati, realizzata con 2 chilometri di fibra ottica attorcigliata in una bobina quadrata di 1,4 metri di lato) a diverse ore, consentendo tempi di misura stabili di quasi un giorno intero, così rilevando un numero di fotoni in quantità e qualità sufficiente a ottenere questa notevole precisione (per uno stato così fragile). Da notare che la suddetta stabilità raggiunta è unica per un interferometro Sagnac in fibra ottica di tale dimensioni, per di più considerando il fatto che la fibra è stata attorcigliata a mano senza l’ausilio di macchine automatiche! Ci tengo a precisare che nel nostro esperimento il limite di Heisenberg non è stato raggiunto, né un vantaggio quantistico incondizionato nell’utilizzo di stati NOON a due fotoni rispetto a stati a singolo fotone (considerando lo stesso numero di fotoni rilevati durante l’intero corso della misura) è stato dimostrato. Il passo in avanti è esclusivamente dovuto all’aver raggiunto una tale precisione utilizzando stati entangled in un interferometro così grande e quindi con un’interazione così prolungata fra i fotoni e un ambiente esterno ostile, che provoca un enorme numero di perdite. Il segreto è stato nell’aver raggiunto una stabilità tale nel lungo periodo, grazie all’introduzione di uno switch ottico, per poter aumentare significativamente il tempo di misura e la quantità di fotoni rilevati compensando l’effetto delle perdite».
Come avete fatto a isolare il segnale di rotazione della Terra?
«Come anticipato, la svolta sotto vari punti di vista per noi è stata l’introduzione di uno switch ottico che divide e connette due bobine di fibra da 1 chilometro ciascuna (lunghezza totale 2 chilometri). Siamo quindi riusciti a scambiare la direzione di propagazione dei due fotoni (che si propagano in direzioni opposte) per metà della lunghezza di propagazione nella fibra ottica. Ciò significa che quando i fotoni tornano al punto di partenza il ritardo che hanno accumulato (fase di Sagnac), che quantifica la velocità di rotazione della Terra, è nullo. Quindi, anche se l’interferometro ruota con la Terra, l’effetto indotto dalla rotazione terrestre viene annullato, creando così uno stato di riferimento per estrarre il segnale rotazionale costante di interesse che altrimenti sarebbe stato sempre presente come segnale di fondo. In altre parole è come avere due interferometri Sagnac identici e sovrapposti e sommare i loro segnali, scambiando a comando la direzione di propagazione dei fotoni solo in uno di essi il segnale complessivo è doppio o nullo per via del cambio di segno del segnale di fase in uno di essi. Mi piace dire scherzosamente di avere ingannato la luce facendole credere di trovarsi in un universo non rotante. Questa aggiunta è importante non solo perché consente di confrontare il comportamento dello stato entangled da un sistema di riferimento rotante a uno effettivamente non rotante, ma comporta anche diversi vantaggi tecnici come la soppressione del rumore a bassa frequenza (si può modulare la velocità dello switch a frequenze anche molto elevate) e una maggiore stabilità a lungo termine. Quantificando, la stabilità a lungo termine ottenuta senza e con lo switch ottico a una velocità di modulazione del segnale nell’ordine degli Hz è passata da un minuto a quasi un giorno».
In conclusione, cosa siete stati in grado di osservare?

Raffaele Silvestri, primo autore dell’articolo pubblicato su Science Advances. È dottorando all’università di Vienna nel gruppo di ottica quantistica sperimentale diretto da Philip Walther. Si è laureato all’università di Roma “La Sapienza” discutendo una tesi di metrologia quantistica su chip fotonici integrati. Crediti: R. Silvestri
«Abbiamo osservato l’effetto della rotazione terrestre su uno stato di due fotoni entangled, ovvero l’introduzione di uno sfasamento relativo nello stato quantistico causato dall’effetto Sagnac (un effetto predetto dalla relatività speciale) che è raddoppiato in grandezza rispetto al caso “classico” in cui un fascio laser o singoli fotoni indipendenti e scorrelati (in assenza di correlazioni di natura quantistica) fossero stati utilizzati nella misura interferometrica (effetto di super-risoluzione). L’effetto osservato risiede quindi all’interfaccia fra la relatività speciale e la meccanica quantistica (compatibile con la teoria quantistica dei campi). Se confrontiamo la precisione con quella che possono raggiungere i moderni giroscopi ottici (sensori di rotazione “classici” che operano con fasci laser), siamo ancora lontani. In particolare, i giroscopi laser (ring laser gyroscopes) sono in grado di percepire anche le minime variazioni della velocità di rotazione della Terra e dell’orientamento del suo asse (dovuta ad esempio al moto delle maree) e questa sensibilità è di ordini di grandezza superiore alla nostra (vedi progetto Ginger/Ino dell’Infn). Ciò che è notevole è la precisione che abbiamo raggiunto nel misurare una velocità di rotazione con l’entanglement quantistico, in particolare con uno stato quantistico di due fotoni massimamente entangled. Una domanda che viene naturale porsi è perché non sfruttare l’enorme sensibilità, precisione, accuratezza e stabilità di tali strumenti già operativi e sondarli con fotoni entangled. La risposta è che queste sono cavità ottiche che selezionano una lunghezza d’onda ben precisa e di conseguenza quasi tutti i fotoni, avendo una larghezza di banda spettrale molto maggiore, sarebbero filtrati dalla cavità e perduti. Per questo riteniamo che l’approccio in fibra ottica sia il più promettente se si vogliono spingere i limiti di precisione raggiungibile con stati entangled di singoli fotoni».
Cosa comporta il risultato ottenuto rispetto a esperimenti futuri?
«Un seguito naturale a questo esperimento potrebbe essere l’utilizzo di un altro effetto quantistico senza analogo classico, come ad esempio l’effetto Hong-Ou-Mandel, che può essere osservato inviando due fotoni indistinguibili (non è necessario che siano entangled) nell’interferometro. Questo manterrebbe la natura quantistica dell’esperimento, ma allo stesso tempo potrebbe aumentare ulteriormente la sua sensibilità andando a misurare il ritardo temporale, invece dello sfasamento, fra i due fotoni che si propagano in sensi opposti. Inoltre, la piattaforma interferometrica e lo schema sperimentale è abbastanza flessibile da consentire ulteriori test con molti altri stati quantistici a più fotoni. Alcuni di essi sono più resistenti alle perdite di fotoni rispetto agli stati NOON e potrebbero in linea di principio dimostrare un vantaggio quantistico incondizionato, aumentando al contempo la precisione della misura grazie al flusso di fotoni più elevato. In ogni caso, il passo successivo sarebbe quello di aumentare la precisione di una quantità significativa tale da poter rilevare effetti gravitazionali come l’effetto geodetico (o precessione di de Sitter) e di frame-dragging (o precessione di Lense-Thirring) su una coppia di fotoni entangled. Si tratta di effetti gravitazionali previsti dalla teoria generale della relatività di Einstein in presenza di un corpo massiccio statico (geodetico) e rotante (frame-dragging, cioè la Terra in rotazione “trascina” la sua curvatura dello spaziotempo) e si manifesta semplicemente come una piccola correzione della velocità di rotazione della Terra. Questa misura rappresenterebbe il primo test sperimentale del comportamento di un fenomeno quantistico fondamentale come l’entanglement in uno spaziotempo curvo come descritto dalla teoria della gravitazione di Einstein, facendo luce su questo regime inesplorato dove le due teorie fondamentali si incontrerebbero, e forse in un futuro non così lontano».
Per saperne di più:
- Leggi su Science Advances l’articolo “Experimental Observation of Earth’s Rotation with Quantum Entanglement” di R. Silvestri, H. Yu, T. Strömberg, C. Hilweg, R. W. Peterson, P. Walther






